Tran H, Xie D, Liaw P K, et al. Mechanistic cohesive zone laws for fatigue cracks: Nonlinear field projection and in situ synchrotron X-ray diffraction (S-XRD) measurements [J]. Journal of the Mechanics and Physics of Solids, 2025, 196: 106010.
Tran, H., et al. "Mechanistic cohesive zone laws for fatigue cracks: Nonlinear field projection and in situ synchrotron X-ray diffraction (S-XRD) measurements." Journal of the Mechanics and Physics of Solids 196 (2025): 106010.
Tran, H., Xie, D., Liaw, P. K., Chew, H. B., & Gao, Y. F. (2025). Mechanistic cohesive zone laws for fatigue cracks: Nonlinear field projection and in situ synchrotron X-ray diffraction (S-XRD) measurements. Journal of the Mechanics and Physics of Solids, 196, 106010.
背景简介
内聚区模型(cohesive zone model)通过预设裂纹面间的界面应力—张开位移关系,模拟裂纹扩展并确定裂纹阻力,被广泛应用于单调或循环载荷下的断裂分析。但在疲劳裂纹扩展研究中,现有的内聚区模型对加载—卸载不可逆性和滞后现象的描述仅为假设(如假设单一卸载路径或简化的滞后曲线),缺乏直接的试验测量验证,无法明确其与微观损伤机制的关联。
此外,对于疲劳裂纹尖端的建模,现有的方法存在诸多局限性,比如:将裂纹尖端由孔洞形核/长大、位错演化等复杂损伤机制主导的“复杂”过程区临时简化为内聚区模型,这种自上而下的方法多依靠现象学描述,往往基于经验校准,与微观损伤机制的联系模糊;抑或是从微观缺陷(如孔洞、位错)演化推导一定的内聚区规律,但这种自下而上的方法受限于计算能力,难以穷尽所有缺陷的贡献,可行性较低。
本文旨在利用原位同步辐射X射线衍射获取应变场,通过逆方法重建疲劳裂纹的内聚区规律,即明确其峰值界面应力、内聚能、张开位移量等参数,及其与“复杂”过程区微观机制的定量关联,提取内聚区规律的函数形式,实现由试验直接确定机械内聚区规律。
成果介绍
(1)研究以细晶粒ZK60镁合金为对象,利用S-XRD技术获得了裂纹尖端不同载荷下的高分辨率弹性应变场,其光束尺寸与材料晶粒尺寸及塑性区尺度相匹配,能够覆盖“复杂”过程区和以塑性变形为主导的“简单”过程区。
.png)
图1 CT试样示意图以及循环载荷示意图,图中裂纹尖端附近红色虚线区域为应变映射区域
.png)
图2 使用同步加速器X射线衍射(S-XRD)技术进行应变映射测量的衍射测量设置示意图,其中x表示裂纹扩展方向,y表示裂纹张开方向。在非线性场投影方法中,采用最后一个循环中的完全卸载状态作为参考构型。利用Debye-Scherrer环的畸变提取弹性应变张量
.png)
图3 不同载荷水平下距裂纹尖端距离测量的弹性应变εelαβ(x,y)等值线:(a-d, m-p)沿着裂纹扩展方向应变 (Exx:εelxx);(e-h, q-t)沿裂纹张开方向沿着应变 (Eyy:εelyy);(i-l, u-x)裂纹尖端的剪应变 (Exy:εelxy)
(2)由于试验获得了稳态疲劳裂纹扩展阶段最后一个循环内不同载荷阶段的完整弹性应变图谱。因此,在非线性场投影方法的基础上,研究将材料参考构型设定为最后一个疲劳循环结束时的状态,此时载荷完全卸载至零,然后按时间顺序逆向追溯,即可将该特定循环内的变形可视为线性弹性的。首先定义一个扣除残余应变的新应变场:
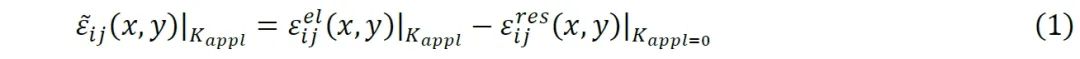
其中εelij(x,y)|kappl代表最后半个加载循环中的kappl≠0的弹性应变场,εresij(x,y)|kappl=0代表加载最后一个点处的残余应变场,加载情况图见图2左下。
由此得到应力场:
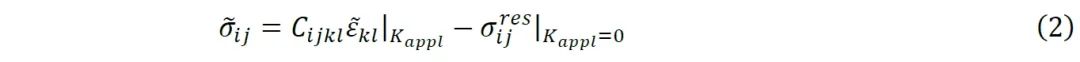
.png)
图4 用非线性场投影法重建疲劳裂纹尖端内聚区规律的裂纹尖端附近三种不同区域的示意图
为重建相应的位移场,研究选取裂纹尖端近似位置(x=y=0)为中心,忽略“复杂”过程区高不确定性的应变数据,假设边界节点位于K主导区内,得到位移场公式如下,结果如图5。
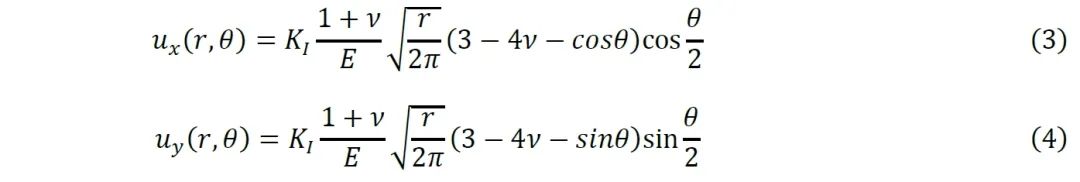
.png)
图5 单个加载和卸载循环期间不同载荷水平下的位移等值图
为求得裂纹尖端的内聚区规律,首先将通过非线性场投影方法提取,借助Maxwell-Betti互易定理,将过程区外部的测量数据(图 4中的路径∂R2)与裂纹面沿线的等效界面应力及张开位移分布(图 4中的路径∂R1)关联起来。考虑先前得到的应力场σ~(x,y:Kappl)与辅助应力场σ^ij,有:
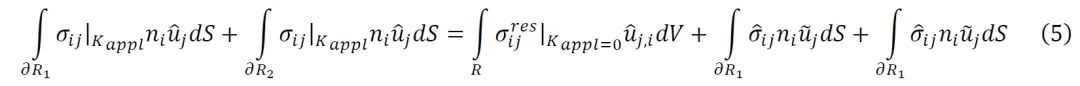
进一步简化为:
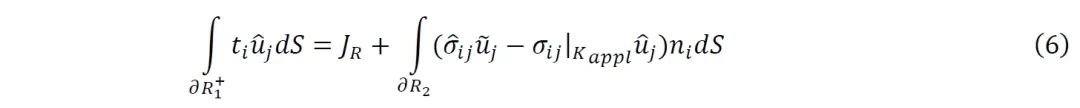
其中裂纹面界面应力ti=σij|kapplni,此外对于上未知的界面应力可通过傅里叶级数来表示:
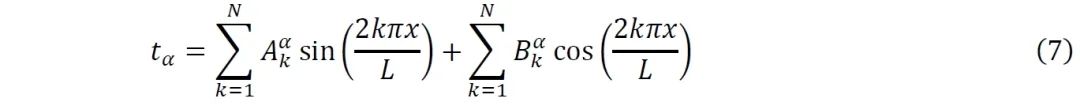
其中通过辅助预设的辅助场来求解系数,进而得到界面应力分布。
根据上述推导,研究给出的重建步骤为:
a) 在∂R内准备若干辅助线弹性场“^”与各种调和边界条件。
b) 将S-XRD测量结果集合到“~”场中。
c) 结合公式(6)和公式(7),选取确定的一个辅助场,求得傅里叶系数。该步骤中的JR由图2左下施加载荷图中最后一点测得的应力场确定;σij|kappl由S-XRD测量结果中线弹性材料的本构矩阵Cijkl确定;由弹性应变场和应变与位移之间的有限元插值函数求得(公式(3)与公式(4))
d) 在重建沿∂R1的t2分布后,借助线性弹性有限元模拟,通过∂R1⁺和∂R1⁻处的位移跳跃来计算张开位移量。具体实施步骤为:在与K主导区尺寸相同的有限元模型上施加沿∂R1得到的界面应力,模型边界节点位移与式(3)和式(4)中的位移相同,并将式(2)中的残余应力场作为初始残余场。此时,张开位移δ2即为沿∂R1的位移u2的两倍
(3)研究发现在加载和卸载阶段,界面应力均从零点快速上升至峰值(集中在x≈0.2 mm处),随后逐渐下降至恒定值;张开位移则单调衰减至零,但在x≈0.2 mm以外衰减速率放缓。相同载荷下(如0.75Pmax),卸载时的界面应力略低于加载状态,而张开位移略高,表明疲劳导致应力承载能力下降,且这种差异随载荷降低(如0.5Pmax)进一步扩大,证实非线性场投影方法可量化疲劳不可逆损伤(如图6)。
.png)
图6 用非线性场投影法重建了加载和卸载循环过程中的界面应力和张开位移的分布
研究还发现在加载阶段,界面应力-张开位移关系呈线性关系。界面应力快速达到峰值后,以恒定斜率随张开位移增大降至零。但在卸载阶段则呈现出双线性特征:从P/Pmax=1至0.75时,斜率陡峭,对应不可逆疲劳损伤;从0.75至0.5时,斜率平缓,接近加载阶段,体现弹性卸载特性(图8 (a))。这种线性再加载与双线性卸载的组合形式(图 7 (b4))与以往模型截然不同。同时在沿着裂纹面的不同材料点上也始终观察到这种线性再加载、双线性卸载的内聚力响应(图8 (b))。研究判断该形式可能与氧化层(对应卸载阶段)和位错塑性(对应再加载阶段)相关联。对于其他具有不同耐腐蚀性和存在空洞等多种损伤过程的合金,其疲劳裂纹内聚力区规律也可能有所不同。
.png)
图7 疲劳内聚区规律的数种函数形式
.png)
图8 用非线性场投影法重建了 (a) 加载和卸载循环过程中沿着裂纹前缘的界面应力-张开位移关系和 (b) 考虑残余应力影响的疲劳裂纹扩展内聚区演化结果
致谢
本合作研究得到美国国家科学基金会的支持,分别向伊利诺伊大学(项目编号 DMR 1809696)和田纳西大学(项目编号 DMR 1809640)提供了资助。Xie博士和Gao感谢阿贡国家实验室的Yang Ren博士在衍射测量方面给予的指导,以及田纳西大学的Brett G. Compton教授所提供的富有成效的讨论。本研究使用了先进光子源的资源,该设施是美国能源部科学办公室用户设施,由阿贡国家实验室根据合同编号 DE-AC02-06CH11357 为美国能源部科学办公室运营。本文第一作者:H. Tran (University of Illinois at Urbana-Champaign),D. Xie(University of Tennessee),本文通讯作者:H.B. Chew(University of Illinois at Urbana-Champaign),Y.F. Gao(University of Tennessee)。
本期小编 周子尧(整理)
董乃健(校对)
程 航 (审核)
董乃健(发布)
|