Grant C, Roongta S, Burnett T L, et al. Simulating hydrogen-controlled crack growth kinetics in Al-alloys using a coupled chemo-mechanical phase-field damage model[J]. Acta Materialia, 2025, 284: 120597.
Grant, C., et al. "Simulating hydrogen-controlled crack growth kinetics in Al-alloys using a coupled chemo-mechanical phase-field damage model." Acta Materialia 284 (2025): 120597.
Grant, C., Roongta, S., Burnett, T. L., Prangnell, P. B., & Shanthraj, P. (2025). Simulating hydrogen-controlled crack growth kinetics in Al-alloys using a coupled chemo-mechanical phase-field damage model. Acta Materi
alia, 284, 120597.
背景简介
第三代锌含量更高的7xxx系列Al-Zn-Mg合金理论上具有比成熟材料(如AA 7050-T7651)更高的强度,并能够提高其在较厚截面零件中的韧性和抗疲劳裂纹扩展性能,同时保持足够的环境辅助开裂(Environmentally Assisted Cracking, EAC)性能。然而研究发现现有的第三代7xxx 系列铝合金在暴露于温湿空气中时易发生EAC,且其开裂过程呈现高度脆性特征,开裂路径几乎完全沿晶界延伸。这是由于当暴露的晶界与湿空气中的水分发生反应生成氢时,会引发局部化学反应,该反应会导致合金脆化,其主要机制为氢增强内聚失效。本研究采用晶体塑性化学-力学耦合相场断裂模型,结合真实多晶晶粒结构,对7xxx系铝合金中微观结构尺度短裂纹的EAC扩展速率控制过程进行了评估。与以往研究相比,该模型通过引入具有可调节衰减时间(用于表征钝化)的源项,更准确地复现了裂纹尖端氢生成的效应。将模型中的氢源项与文献中已有的其他输入参数进行对比后发现,模型预测的裂纹扩展行为与试验观测结果在定性层面具有良好的一致性。
成果介绍
(1)本文所构建的相场损伤模型以吉布斯自由能泛函为基础,整合机械变形、损伤演化与氢传输三大物理过程,最终在多物理场模拟框架DAMASK中实现。模型的理论基础是吉布斯自由能泛函,其总自由能由力学贡献(ψmech)、损伤贡献(ψdam)与化学贡献(ψchem)三部分叠加,表达式如下:
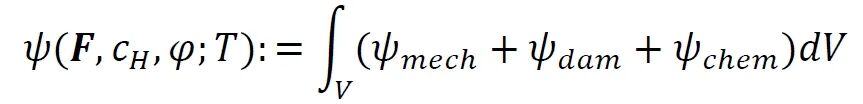
其中,F为变形梯度张量,cH为氢浓度场,φ为相场损伤变量,T为绝对温度。该泛函通过耦合三者的相互作用,量化EAC过程中“应力-氢-裂纹扩展”的关联机制。
对于力学部分建模,其核心是描述材料在载荷与氢作用下的变形行为,分为变形梯度分解、晶体塑性模型与化学-弹性耦合三部分。变形梯度分解指将材料总变形梯度分离弹性、氢致本征应变与塑性变形的贡献,相关表达式如下:
.png)
其中,Fp为塑性变形梯度,代表晶格不变的等容滑移变形;Fi为本征应变梯度,由氢溶解引起的体积错配导致;Fc为弹性变形梯度,描述材料的弹性响应。
晶体塑性模型部分采用Hutchinson开发、Kalidindi扩展的唯象晶体塑性模型,核心是通过滑移系剪切速率描述塑性变形。由于晶体材料的塑性发生在特定的变形系统上,取决于晶格结构,因此给出了塑性速度梯度的以下定义,即:
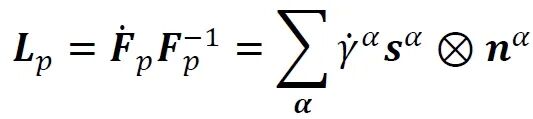
化学-弹性耦合根据氢溶解于铝基体后会引发局部变形导致本征应变,本征应变取决于体积失配系数vH和氢浓度场cH,本征应变可通过其速度梯度来表示,其由下式给出:
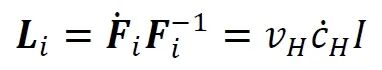
对于损伤建模,采用相场损伤模型模拟沿晶 EAC 的脆性断裂,通过扩散界面近似尖锐裂纹。损伤演化方程如下:
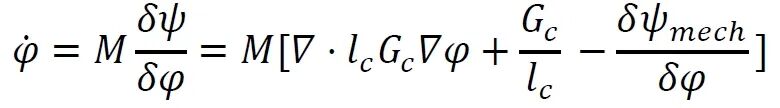
界面能对总自由能的贡献如下:
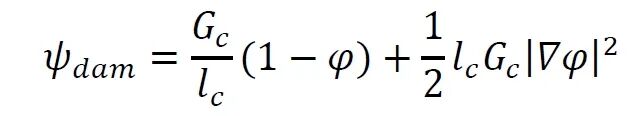
对于化学建模,对总自由能的贡献被定义为不同氢陷阱位置的贡献之和:
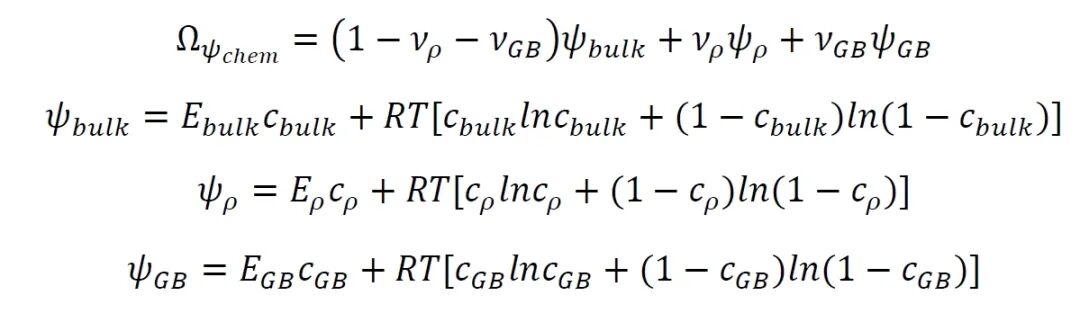
其中Ω是摩尔体积,vρ和vGB是位错核和晶界的体积分数。假设各陷阱与基体间存在局部化学平衡,材料中总氢浓度cH为各陷阱浓度的体积加权平均:
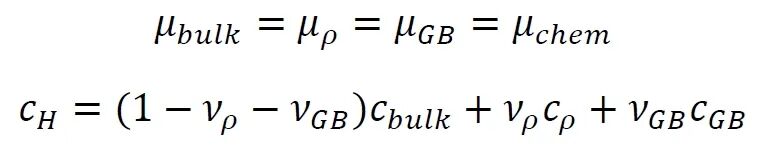
模型包含的氢传输方程遵循添加了源项的Fick定律:
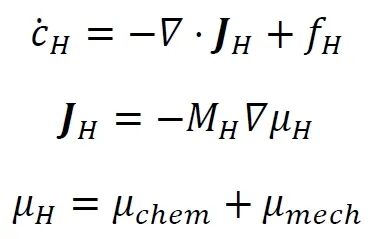
其中MH为晶格固定参考系下的组元迁移率,其与氢扩散系数通过公式M=D/RT相关联(D为氢扩散系数,R为普适气体常数,T为绝对温度),μH为忽略损伤贡献的总化学势,fH为系统中的氢生成源;cH为以摩尔分数表示的氢浓度场。
模型的化学与损伤的耦合部分以临界能量释放率Gc依赖于局部晶界氢浓度的形式实现。其表达式如下:
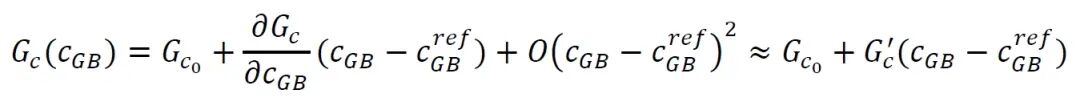
其中MH为晶格固定参考系下的组元迁移率,其与氢扩散系数通过公式M=D/RT相关联(D为氢扩散系数,R为普适气体常数,T为绝对温度),μH为忽略损伤贡献的总化学势,fH为系统中的氢生成源;cH为以摩尔分数表示的氢浓度场。
模型的化学与损伤的耦合部分以临界能量释放率Gc依赖于局部晶界氢浓度的形式实现。其表达式如下:
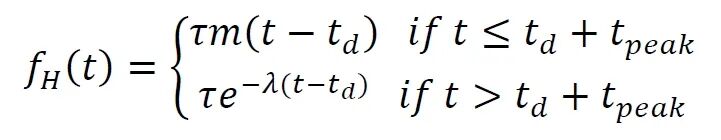
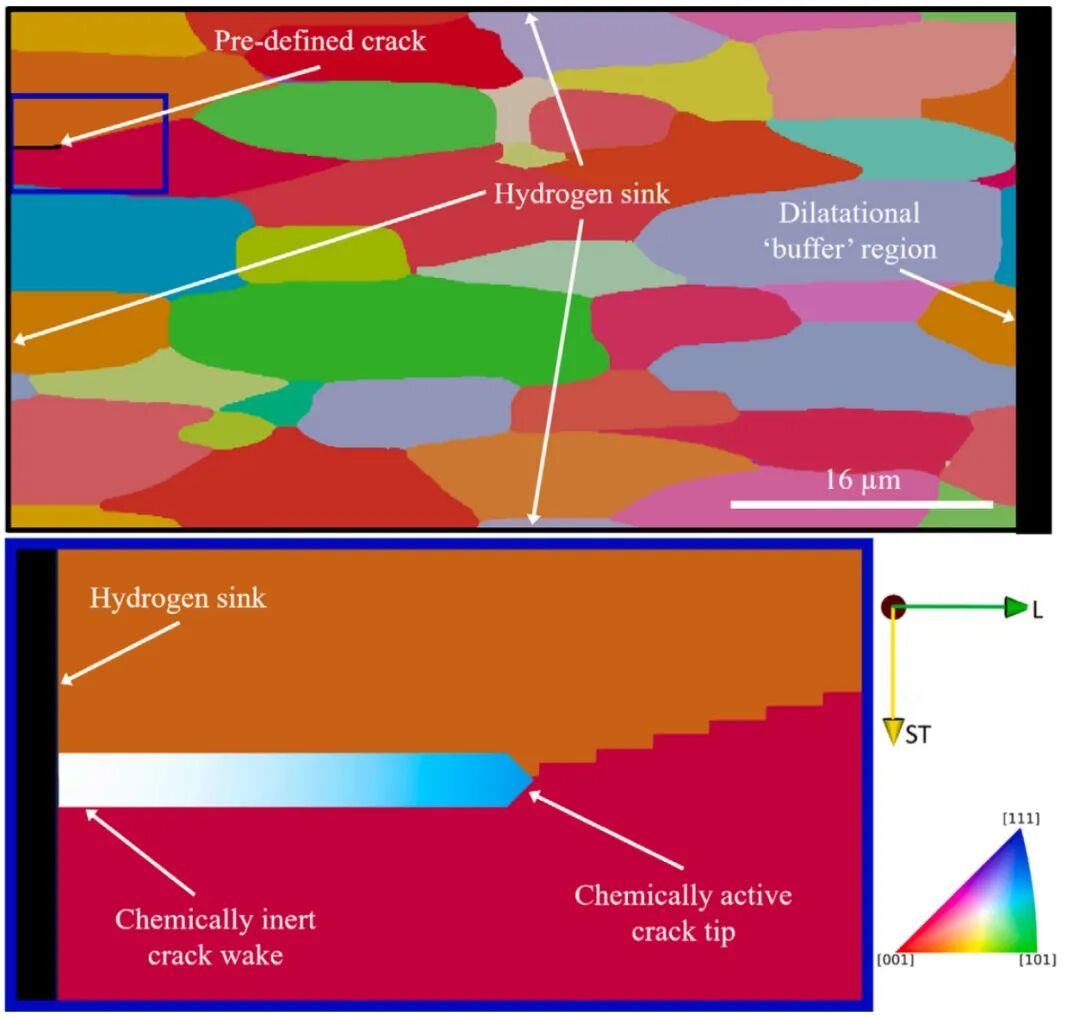
图1 模拟所用的具有预定义初始裂纹的准二维多晶VE,在ST方向上施加单轴加载条件
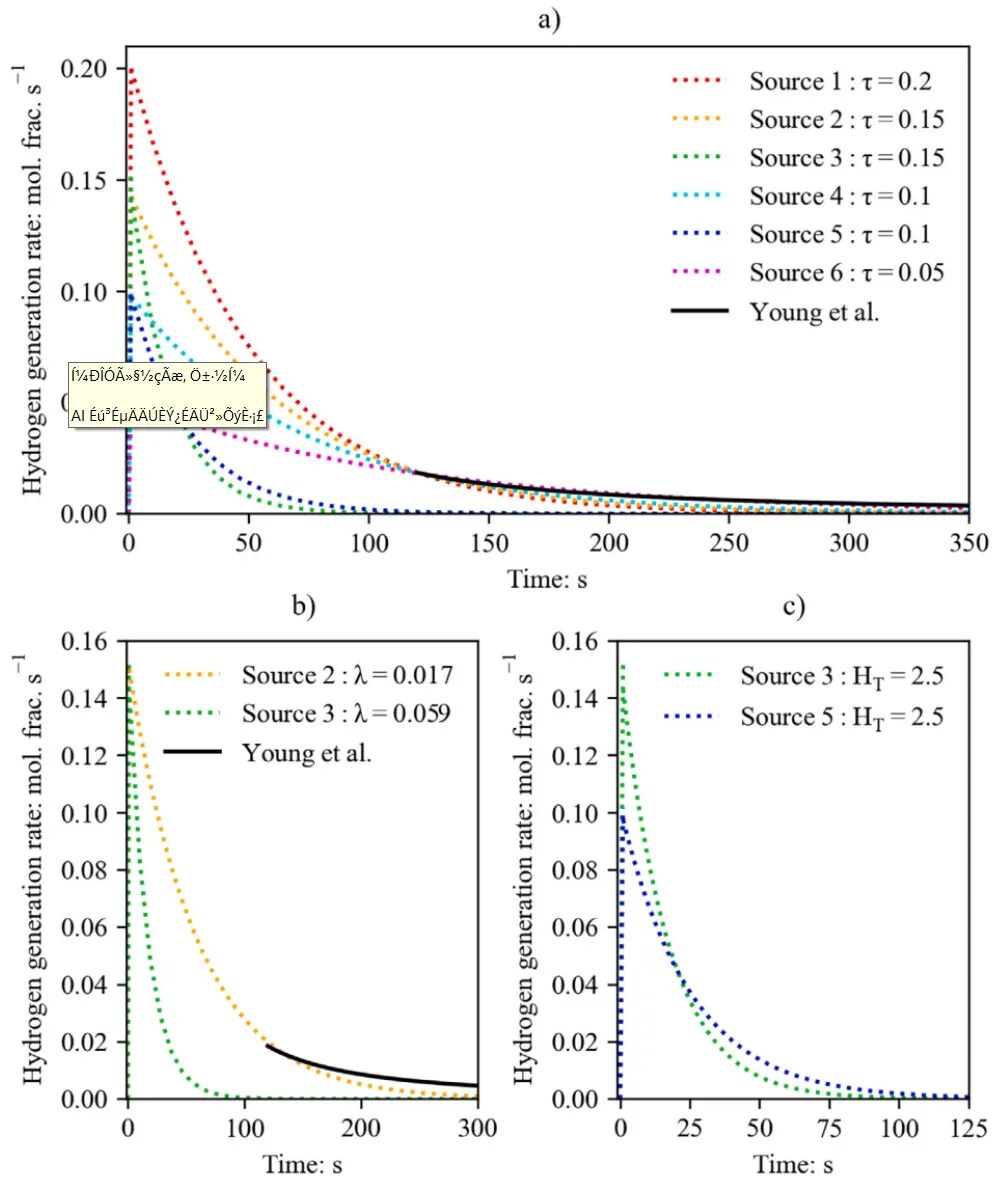
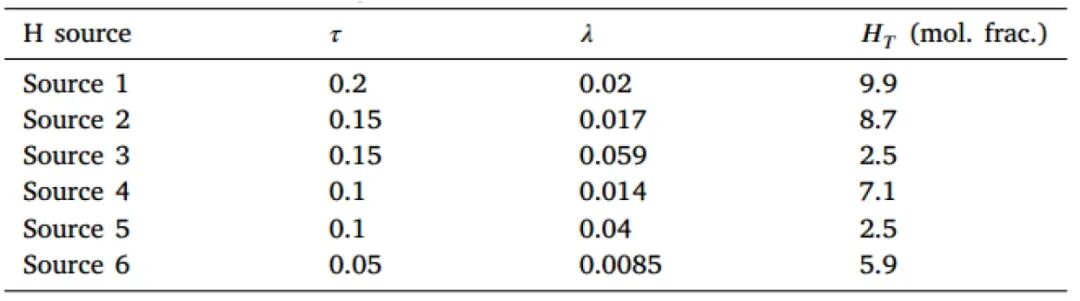
图2 氢生成速率-时间曲线,将模型可调节的裂纹尖端表面氢源行为与Young等人的试验测量结果进行比较
表 1 图2中所示的六种裂纹尖端氢源函数参数
(2)通过施加380 MPa应力与表1氢源Source 4,对VE中预制裂纹的扩展过程进行分析,结果见图3,明确了裂纹尖端区域的多物理场耦合特征。图3a显示裂纹严格沿GB扩展,平均路径遵循最大拉应力平面,但遇到倾斜晶界结时会发生显著偏转,符合7xxx系铝合金EAC的试验观测(沿晶脆性开裂)。图3b显示裂纹尖端应力场同时受到两方面因素的影响:一是由晶界角度导致的裂纹倾斜度,二是局部晶粒结构。综合这些图谱可知,氢浓度升高最显著、捕获能力最强的位点是晶界,但氢浓度最高的地方是氢生成最活跃的裂纹表面单元附近。此外模型预测的位错密度较高的基体区域。如:裂纹尖端塑性区、裂纹尾迹的滑移带,同样对应氢浓度升高的区域。
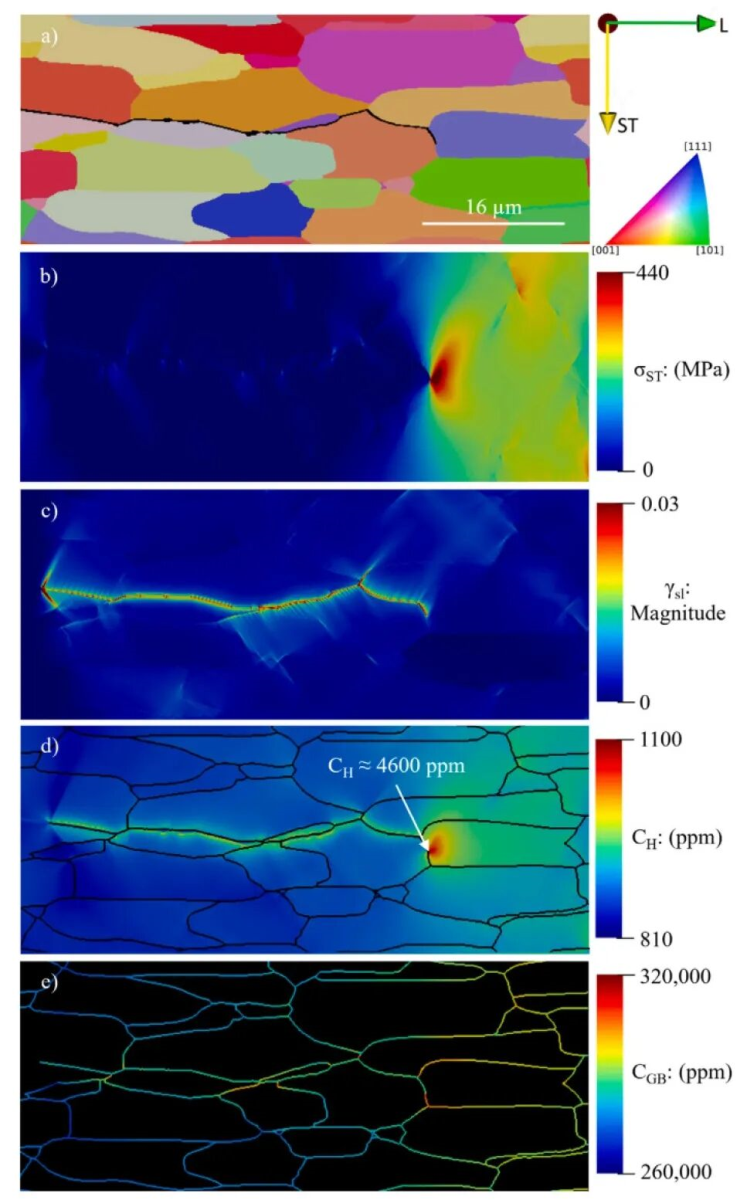
图3 环境辅助开裂(EAC)模拟扩展路径及其相关场变量的快照(a)展示晶粒结构的反极图(IPF);(b)裂纹张开方向的应力分量;(c)塑性滑移量;(d)基体体积平均氢浓度;(e)晶界上氢浓度分布的缩放后氢浓度图
(3)在通过施加317 MPa应力与表1氢源Source 4的随时间模拟裂纹扩展试验中(见图4),当裂纹沿近垂直于载荷方向的优取向扩展时,速度较高;当遇到低长径比晶粒导致路径大幅偏转,瞬时速度与驱动力均显著下降,由此造成新断裂表面生成速率下降,VE中主动产氢的位点随之减少。同时在施加380 MPa 应力与表1氢源Source 1的随时间模拟裂纹扩展试验中(见图5),呈现了符合实际的裂纹分叉行为:首先两条路径均因应力与氢浓度足够而共同扩展,但由于晶粒拓扑差异,其中一条路径先调整至更优载荷取向,应力场开始向该路径集中。这种不对称的应力分布使上方裂纹能够更快地扩展,导致下方分支裂纹处于上方裂纹尖端的尾迹区域,产生应力屏蔽,最终导致劣势路径氢浓度不足、速度下降,最终停滞,仅优势路径持续扩展。该现象与试验中 “EAC 裂纹分叉后多为单分支持续扩展” 的观测完全吻合。
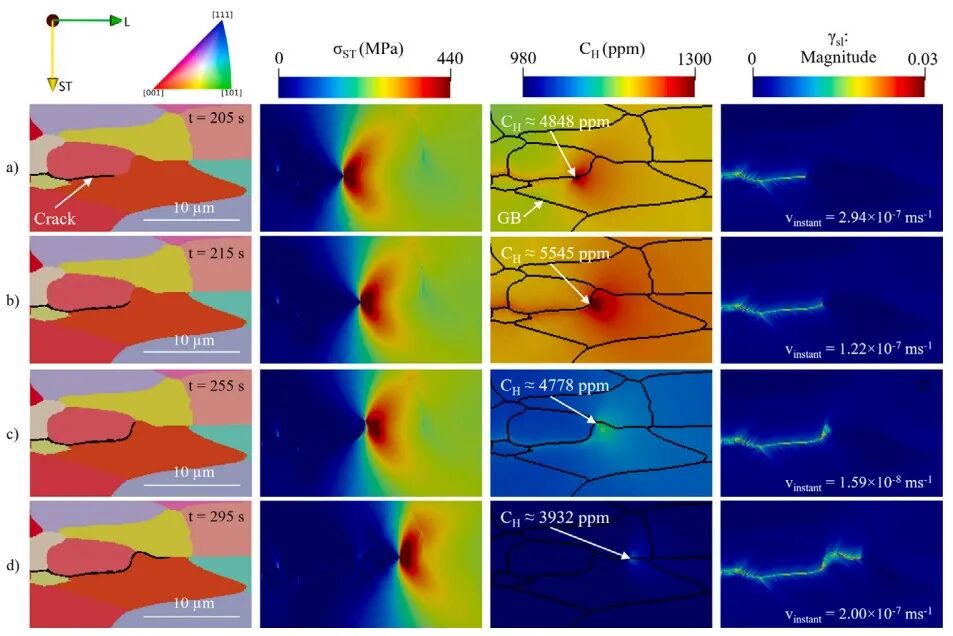
图4 随时间模拟裂纹扩展遇到显著倾斜的晶界平面的过程:裂纹沿不断倾斜的晶界从与施加应力垂直方向(最大驱动力)逐步转变为大致平行的方向(最小驱动力)
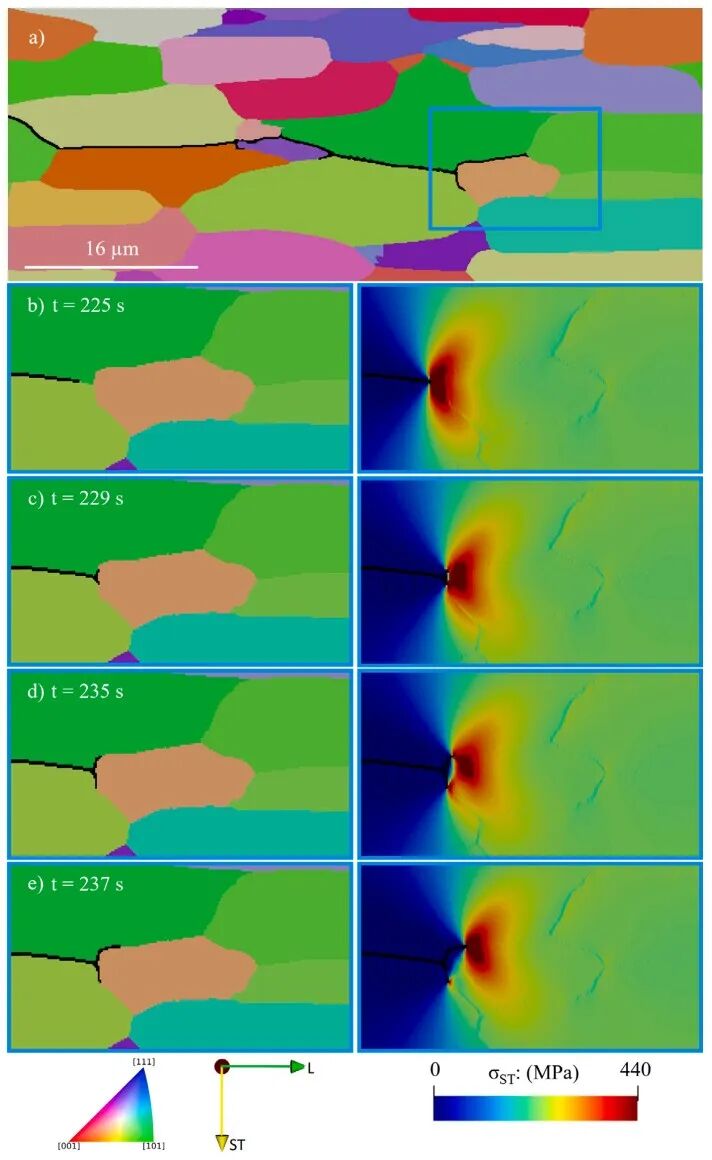
图5 随时间模拟裂纹扩展遇到晶界结分叉的过程
(4)模拟结果发现氢扩散速率远快于裂纹扩展速率(图6),且裂纹尖端到GB的扩散距离仅纳米级,因此传输非速率控制步骤,验证“局部氢生成主导EAC”的假设。此外通过进一步模拟发现裂纹尖端氢源的定义对预测裂纹扩展速率具有显著影响(图7)。同时对比图8可以发现,氢的产生总量似乎比峰值产生速率更重要,这是因为氢的扩散速率比裂纹扩展速率高,因此需要高速率的氢供应来维持裂纹扩展。但是,氢源的峰值强度和产生的总生成量之间可相互补偿。
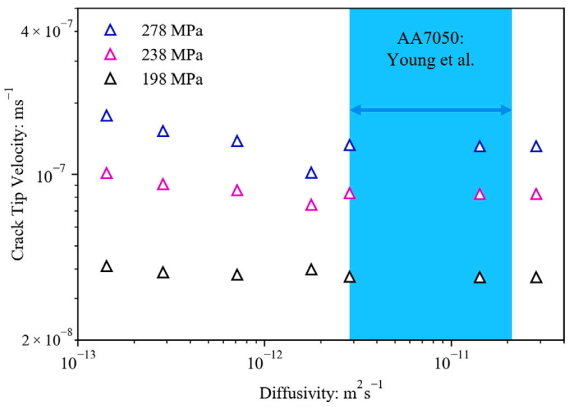
图6 氢扩散系数对裂纹尖端速度的影响
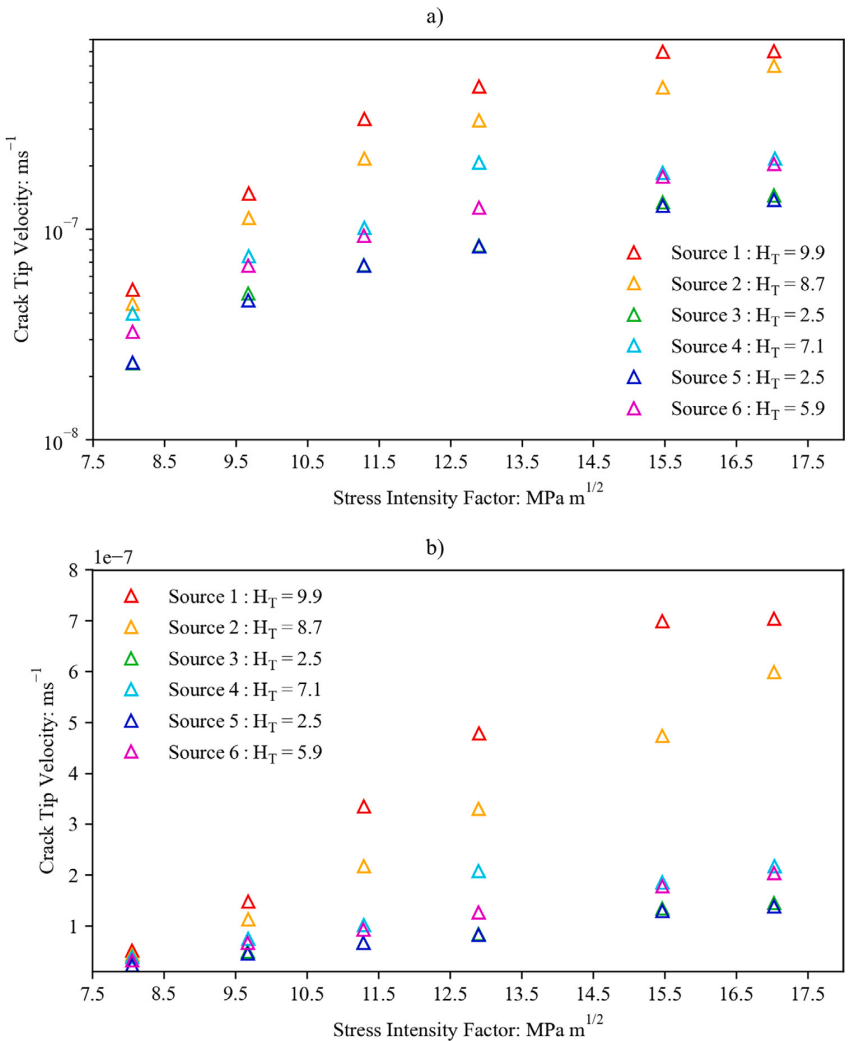
图7 六种裂纹尖端氢源的裂纹尖端速度-应力强度因子曲线:(a)速度轴采用对数刻度,(b)速度轴采用线性刻度
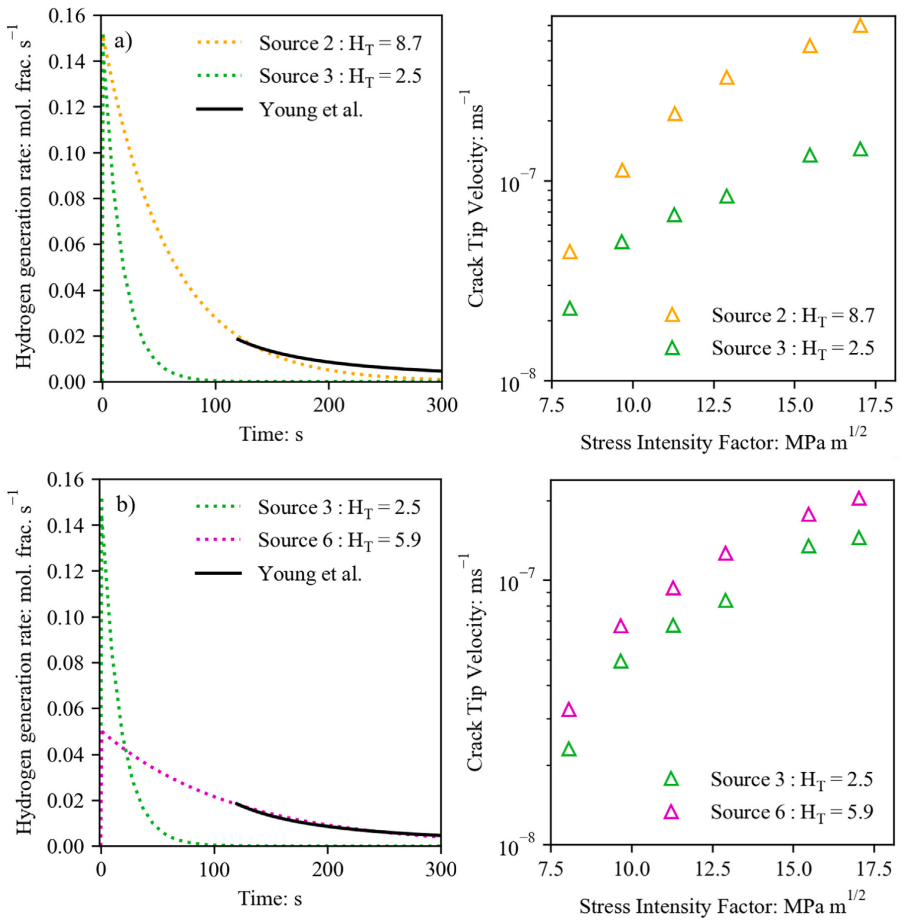
图8 不同氢源的氢生成速率-时间曲线及对应裂纹尖端速度-应力强度因子曲线
(5)通过与Euesden等人发表的70℃ 85%RH 4PB测试结果进行对比验证可以看出,在短裂纹向长裂纹过渡的整个区间内,模拟结果与试验结果展现出相似的v-KI响应特征,模型预测的总体趋势显示出良好的一致性。
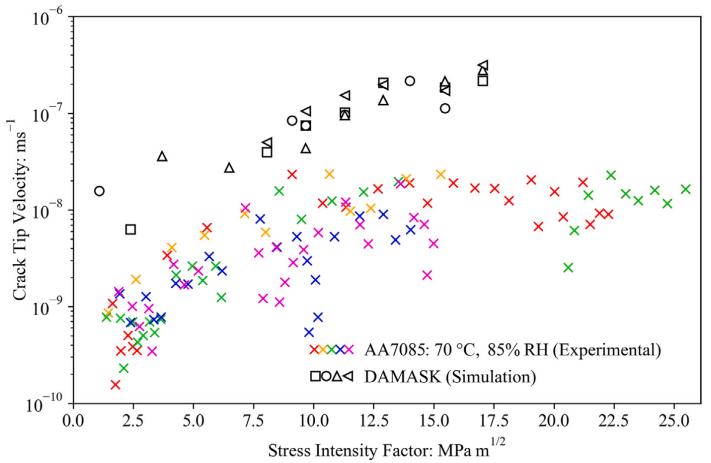
图9 模拟结果与实际试验的裂纹尖端速度-应力强度因子关系对比图
致谢
感谢英国皇家工程院与英国空客公司,感谢二者通过“空客-曼彻斯特大学冶金卓越中心”提供的资金支持。作者同样感谢英国工程与物理科学研究委员会(EPSRC)提供的以下资助:LightForm项目基金(编号:EP/R001715/1)、Metallic Systems CDT,编号:EP/L016273/1,以及Henry Royce Institute for Advanced Materials-该研究所的资助来自英国工程与物理科学研究委员会的多项基金(编号分别为:EP/R00661X/1、EP/S019367/1、EP/P025021/1、EP/P025498/1),这些资助为本次研究的相关工作提供了支持。作者还感谢曼彻斯特大学的Computational Shared Facility,以及谢菲尔德大学的 Stanage HPC facility为本研究提供的计算资源支持。本文第一作者和通讯作者:C. Grant(University of Manchester)。
本期小编 周子尧(整理)
董乃健(校对)
程 航(审核)
董乃健(发布)
|